Let's have a look at some more traversals which are not that standard but will help you to expand your control over Binary trees.
Spiral Traversal
In this traversal, we need to print the nodes in a zig-zag format.
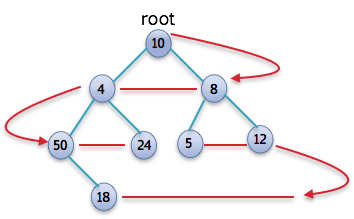
As you can see in the above example the tree is traversal fir left to right and then right to left.
Intuition --> As we can observe that this traversal is very much close to level order traversal, we just need to reverse some levels and as we can see that every alternate level is reversed.
Implementation --> To implement the solution we can simply traverse the tree level wise and we can keep a boolean flag to decide whether to reverse the level or not.
Edge cases --> The only edge case here is that if the root is null then in that case our traversal list will be empty.
vector<int> zigZagTraversal(BinaryTreeNode<int> *root){
vector<int> ans;
if(root == nullptr) return ans;
bool isreverse = false; // This flag will help us to decide whether to reverse the level or not.
//Rest is simple level order traversal.
queue<BinaryTreeNode<int> *> q;
q.push(root);
while(!q.empty()){
int size = q.size();
vector<int> temp;
while(size--){
BinaryTreeNode<int> *curr = q.front();
q.pop();
if(curr->left) q.push(curr->left);
if(curr->right) q.push(curr->right);
temp.push_back(curr->data);
}
if(isreverse){
reverse(temp.begin(), temp.end());
}
isreverse = !isreverse;
ans.insert(ans.end(), temp.begin(), temp.end());
}
return ans;
}
If you don't know level order traversal or want to revise other standard traversals here is the link Introduction to Binary Trees.
Boundary Traversal
In boundary traversal, we traverse around the boundary of the tree.

In the above example, we can see that first, we need to traverse the left then all the leaves and then the right.
Intuition --> As we can observe that we first need to add all the extreme left nodes and then all the leaf nodes and then all the extreme right nodes so we can probably use any of the DFS traversals. We decided to go with DFS, not BFS because we need to go deep in the extreme left and then extreme right. Since we do not have any standard traversal which can give us extreme rights and extreme lefts we need to tweak those traversals to get our desired solution
Implementation --> To implement the solution we can implement three functions one for left boundary nodes, one for right boundary nodes and another for leaf nodes and then we can combine all three and get our boundary traversal list.
Edge cases --> The only edge case here is that if the root is null then in that case our traversal list will be empty.
void addLeftBoundary(TreeNode<int>* root, vector<int> &boundary){
// Function to get all the extreme lefts
if(root == NULL or (root->left == NULL and root->right == NULL)){
return;
}
boundary.push_back(root->data);
if(root->left != NULL) {
addLeftBoundary(root->left, boundary);
} else{
addLeftBoundary(root->right, boundary);
}
}
void addRightBoundary(TreeNode<int>* root, vector<int> &boundary){
// Function to get all the extreme rights
if(root == NULL or (root->left == NULL and root->right == NULL)){
return;
}
if(root->right != NULL){
addRightBoundary(root->right, boundary);
} else{
addRightBoundary(root->left, boundary);
}
boundary.push_back(root->data);
}
void addLeavesBoundary(TreeNode<int>* root, vector<int> &boundary){
// function to get all the leaf nodes
if(root == NULL) return;
if(root->left == NULL and root->right == NULL){
boundary.push_back(root->data);
return;
}
addLeavesBoundary(root->left, boundary);
addLeavesBoundary(root->right, boundary);
}
vector<int> traverseBoundary(TreeNode<int>* root){
vector<int> boundary;
if(root == NULL) return boundary;
boundary.push_back(root->data);
// add left boundary
addLeftBoundary(root->left, boundary);
// add left leaf nodes
addLeavesBoundary(root->left, boundary);
// add right leaf nodes
addLeavesBoundary(root->right, boundary);
// add right boundary
addRightBoundary(root->right, boundary);
// combined boundary
return boundary;
}
Diagonal traversal
Here we traverse diagonally. A diagonal is a line inclined 45°.

In the above example, we can clearly see that we need to traverse right from a node to be in the same diagonal.
Intuition --> As we can observe that we first need to traverse to the right. But while doing so we will lose the entire left subtree. so we need something to store our left nodes so that we can traverse them after we have completed our one diagonal. We can see as well that we would require those nodes first which we encountered first we need that first to start the traversal of our next diagonal so this makes us think about using a queue that is FIFO (first in first out).
Implementation --> To implement the solution we can use a queue data structure to store our nodes which we may need in future and we can traverse the tree in right.
Edge cases --> The first and most important edge case is what about those nodes which are not connected to the left subtree of the root in the above example what about node 16 there is no way to reach there by using 20 so for that we will maintain a size variable which will store the size of the queue at the current time and we will know from the size that there is size number of independent nodes which we need to traverse. Another edge case might be if the root is null then we will simply return the empty list.
Let's code it up
vector<vector<int>> create_daigonal(BinaryTreeNode<int>* root){
vector<vector<int>> daigonal;
if(root == nullptr) return daigonal;
queue<BinaryTreeNode<int>*> q;
q.push(root);
while(!q.empty()){
int size = q.size();
vector<int> temp;
while(size--){
BinaryTreeNode<int>* curr = q.front();
q.pop();
while(curr != nullptr){
if(curr->left) q.push(curr->left);
temp.push_back(curr->data);
curr = curr->right;
}
}
daigonal.push_back(temp);
}
return daigonal;
}
Vertical order Traversal
We need to traverse the Tree vertically imagine a 90° line from every node and that is our vertical line along which we need to traverse

This problem is very much easy but the implementation might take a lot of thinking so let's start.
Intuition --> As we can observe in the picture we need different vertical lines which are mapped to the nodes they cross with. So the first thing that comes to our mind is that we may need a map to store the vertical lines and the nodes. At the same time, we also need a level number. Pretty much what I am thinking is that we can assign a coordinate for every node.
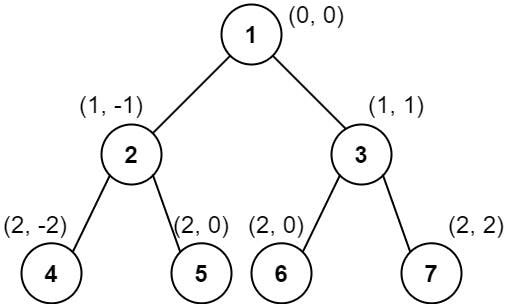
Then for traversing the tree we can use any of the standard traversal methods. I will use in-order as it is recursive and is my favourite.
Implementation --> To implement the solution we need a data structure to store the nodes and the coordinates of the nodes so we can use a map of integers but at the same time we need to store the mapping of the level with the nodes. and since we need to do so we will probably need a map of the map then we also need to store the nodes and there can be multiple nodes for a level do we need a data structure to store that as well I guess we should use multiset for that. so our data structure is ready map<int, map<int, multiset<int>>>. so we are pretty much ready for implementation.
Edge cases --> There are no major edge cases on edge case might be what to do with overlapping nodes and in this case, we have to print both. and the usual edge case if the root is null then return an empty list.
void inorder(TreeNode *node, int level, int vertical, map<int, map<int, multiset<int>>> &ump){
if(node == nullptr) return;
inorder(node->left, level+1, vertical-1, ump);
ump[vertical][level].insert(node->val);
inorder(node->right, level+1, vertical+1, ump);
return;
}
vector<vector<int>> verticalTraversal(TreeNode* root) {
map<int, map<int, multiset<int>>> ump;
vector<vector<int>> ans;
inorder(root, 0, 0, ump);
for(auto x : ump){
vector<int> temp;
for(auto y : x.second){
temp.insert(temp.end(), y.second.begin(), y.second.end());
}
ans.push_back(temp);
}
return ans;
}
There can be more weird traversals but I guess after discussing these traversals we can tackle any traversals.
Things to keep in mind while tackling traversal problems
Always think in terms of standard BFS and DFS traversals.
Then think about the data structures you can use to accomplish your task.
At last think about the edge cases and the optimizations.
Practice Problems
https://www.codingninjas.com/codestudio/problems/reverse-level-order-traversal_764339
https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/
https://www.codingninjas.com/codestudio/problems/diagonal-sum_790722
https://www.codingninjas.com/codestudio/problems/boundary-traversal_790725
https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/
https://www.codingninjas.com/codestudio/problems/diagonal-anagram_794951
