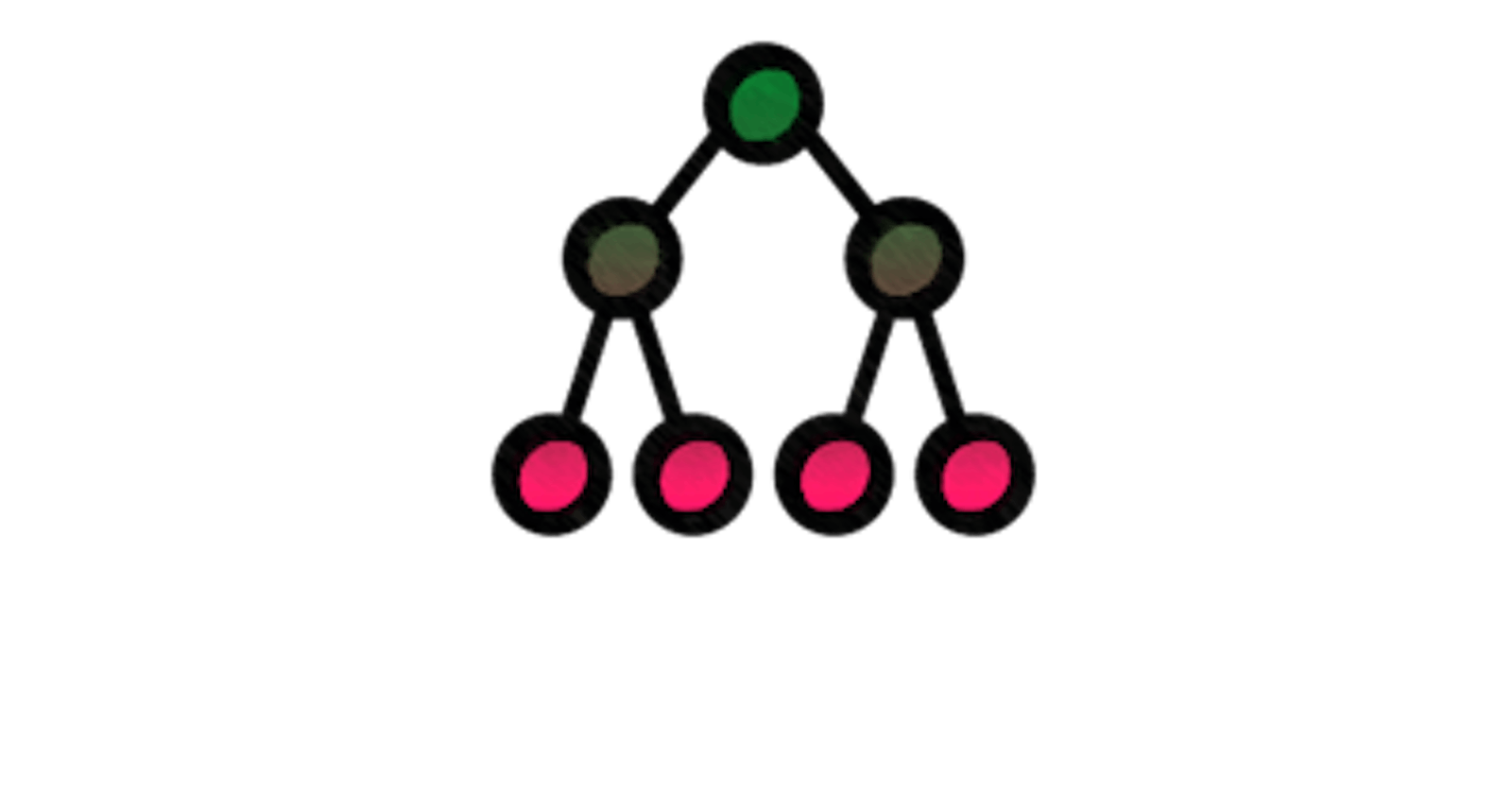
Introduction to Binary Tree

Types of Binary Tree.

Full Binary Tree,
1. Every Node with either 0 or 2 children.
Complete Binary Tree,
1. All levels are filled except the last level.
2. The last level is filled from left to right.
Perfect Binary Tree,
1. All leaf nodes are at the same level.
Balanced Binary Tree,
1. The maximum height of the tree is at max log(n).
Degenerate Tree,
1. It is a skewed tree that looks like a linked list.

Binary Tree Representation

A binary tree consists of three parts,

Left Child,
Node data, and
Right Child.

#include <bits/stdc++.h>
using namespace std;
class Node{
    private:
        int data;
        Node *left_child;
        Node *right_child;
    public :
        Node(){/* do nothing*/}
        Node(int d){
            this -> data = d;
            this -> left_child = NULL;
            this -> right_child = NULL;
        }
};

The above code is the tree class which contains all three components of a tree.

Binary Tree Traversal

There are commonly two types of traversal techniques in binary trees.

Depth-first search (DFS): There are three types of DFS traversal in trees.
1. In order traversal: first visit left, then visit the node and then right.
2. Pre-order traversal: first visit the node, then visit left and then right.
3. Post-order traversal: first visit left, then right and then the node.
Breadth-first search (BFS): There is also a BFS traversal in trees.
1. Level-order traversal: where we traverse the tree level-wise.

Inorder Traversal

void inorder(Node *root){
    if(root == NULL){
        return ;
    }
    inorder(root -> left_child);
    cout << root -> data;
    inorder(root -> right_child);
}

In the above code snippet, a recursive function inorder is used to traverse the tree according to the definition.

First, the left subtree will be traversed, then they root will be printed and then the right subtree will be traversed.

Pre-order Traversal

void preorder(Node *root){
    if(root == NULL){
        return;
    }
    cout << root -> data;
    preorder(root -> left_child);
    preorder(root -> right_child);
}

In the above code snippet, a recursive function preorder is used to traverse the tree according to the definition.

First, the root will be printed, then the left subtree will be traversed and then the right subtree will be traversed.

Post-order Traversal

void postorder(Node *root){
    if(root == NULL){
        return;
    }
    postorder(root -> left_child);
    postorder(root -> right_child);
    cout << root -> data;
}

In the above code snippet, a recursive function preorder is used to traverse the tree according to the definition.

First, the left subtree will be traversed, then the right subtree will be traversed and at last, the root will get printed.

Level-order Traversal

void levelOrder(Node *root){
    if(root == NULL){
        return;
    }
    std :: queue<Node*> q;
    q.push(root);
    while(!q.empty()){
        for(int i = 0; i < q.size(); i++){
            Node* node = q.front();
            q.pop();
            if(node -> left_child != NULL){
                q.push(node -> left_child);
            }
            if(node -> right_child != NULL){
                q.push(node -> right_child);
            }
            cout << node -> data;
        }
    }
    return;
}

In level order traversal we maintain a queue so that we can go back to the parents whose children are still unexplored therefore we maintain a queue we can do this by maintaining the stack also. It's entirely our choice.

Introduction to Binary Tree

For Revision purposes

Table of contents